NGÂN HÀNG CÂU HỎI HỌC PHẦN Giải tích 3
-Mã học phần: MAT2304 -Số tín chỉ: 04 -Ngôn ngữ giảng dạy: Tiếng Việt
Câu hỏi ôn tập
Phần 1. Tích phân suy rộng, tích phân phụ thuộc tham số
Câu 1. Định nghĩa sự hội tụ của các tích phân suy rộng.
Câu 2. Phát biểu và chứng minh tiêu chuẩn Cauchy đối với sự hội tụ của tích phân suy rộng với cận vô hạn.
Câu 3. Phát biểu và chứng minh các dấu hiệu so sánh đối với sự hội tụ của tích phân suy rộng của hàm nhận giá trị dương.
Câu 4. Nêu khái niệm hội tụ tuyệt đối, bán hội tụ của tích phân suy rộng với cận vô hạn.
Câu 5. Phát biểu dấu hiệu Dirichlet đối với sự hội tụ của tích phân suy rộng.
Câu 6. Phát biểu dấu hiệu Abel đối với sự hội tụ của tích phân suy rộng .
Câu 7. Định nghĩa sự hội tụ của tích phân suy rộng đối với hàm không bị chặn. Phát biểu các dấu hiệu so sánh.
Câu 8. Phát biểu và chứng minh tiêu chuẩn Cauchy đối với sự hội tụ của tích phân suy rộng của hàm không bi chặn.
Câu 9. Nêu định nghĩa tích phân phụ thuộc tham số với cận tích phân hữu hạn. Phát biểu định lý về tính khả vi của tích phân phụ thuộc tham số với cận tích phân hữu hạn.
Câu 10. Phát biểu tính định lý về tính khả tích của tích phân phụ thuộc tham số với cận tích phân hữu hạn.
Câu 11. Nêu định nghĩa tích phân phụ thuộc tham số với cận tích phân thay đổi. Phát biểu định lý về tính khả vi của tích phân phụ thuộc tham số với cận tích phân thay đổi.
Câu 12. Nêu định nghĩa tích phân suy rộng với cận vô hạn phụ thuộc tham số, khái niệm hội tụ đều.
Câu 13. Phát biểu tiêu chuẩn Cauchy đối với sự hội tụ đều của tích phân suy rộng với cận vô hạn phụ thuộc tham số.
Câu 14. Phát biểu tính định lý về tính liên tục của tích phân suy rộng với cận vô hạn phụ thuộc tham số.
Phần 2. Tích phân bội, đường, mặt
Câu 15. Nêu định nghĩa phân hoạch hình hộp, đường kính một phân hoạch, phân hoạch mịn hơn.
Câu 16. Nêu cách xây dựng tổng tích phân, định nghĩa giới hạn của tổng tích phân, khái niệm hàm nhiều biến khả tích trên hình hộp.
Câu 17. Chứng minh rằng nếu hàm số f khả tích trên hình hộp D thì f bị chặn trên đó.
Câu 18. Nếu cách xây dựng tổng Darboux trên và tổng Darboux dưới. Phát biểu và chứng minh định lý về điều kiện cần và đủ để một hàm xác định và bị chặn trên hình hộp D là khả tích trên đó.
Câu 19. Phát biểu tiêu chuẩn khả tích Lebesgue.
Câu 20. Định nghĩa tập đo được Jordan. Phát biểu điều kiện cần và đủ của một tập đo được Jordan.
Câu 21. Nêu định nghĩa tích phân trên một tập đo được Jordan.
Câu 22. Phát biểu định lý Fubini.
Câu 23. Phát biểu công thức đổi biến trong tích phân bội.
Câu 24. Nêu khái niệm đường cong. Định nghĩa tích phân đường loại I. Phát biểu và chứng minh điều kiện đủ cho sự tồn tại tích phân đường loại I.
Câu 25. Nêu khái niệm định hướng đường cong. Định nghĩa tích phân đường loại II, mối quan hệ giữa tích phân đường loại I và loại II.
Câu 26. Nêu khái niệm mặt cong, công thức tính diện tích mặt cong.
Câu 27. Định nghĩa tích phân mặt loại I.
Câu 28. Nêu khái niệm định hướng mặt cong. Định nghĩa tích phân mặt loại II, mối quan hệ giữa tích phân mặt loại I và loại II.
Câu 29. Phát biểu các công thức Green, Stokes, Ostrogradski.
đề cương môn GT3 năm 2016
Thông báo ôn lý thuyết cho môn GT1 cho lớp K60A1C
Năm nay, lớp K60A1C (cơ học) sẽ thi chung đề với lớp K60A1T.
Phần lý thuyết các em học từ câu 20 trở đi (cả phát biểu và chứng minh). Các câu từ 1 đến 19 các em học để hiểu.
Chúc các em thi tốt!
NVThu
Seminar Bộ môn Giải tích học kỳ I (2015-2016)
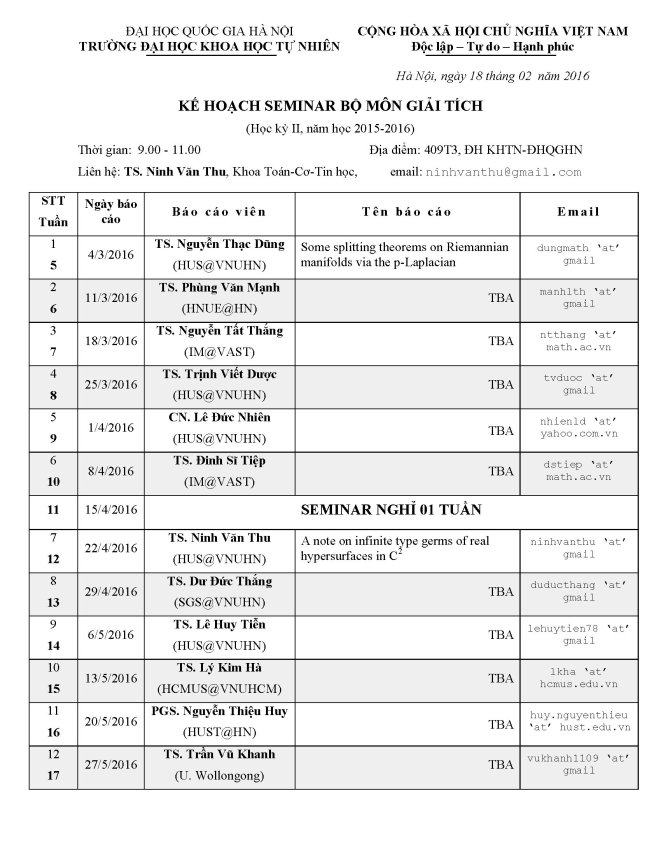
LỊCH SEMINAR BỘ MÔN GIẢI TÍCH
Thời gian: 9.00 – 11.00 am
Phòng 409T3, ĐH KHTN-ĐHQGHN
Liên hệ: TS. Phạm Trọng Tiến, email: phamtien112@gmail.com
1. 18/09/2015: Weighted (LB)-spaces of holomorphic funtcions
TS. Phạm Trọng Tiến (ĐH KHTN-ĐHQGHN)
2. 25/09/2015: Stability results for logarithmic Sobolev and Gagliardo-Nirenberg inequality via mass transport.
TS. Nguyễn Văn Hoàng (Viện Toán học)
3. 2/10/2015: On the Global Stability of the Endemic Equilibrium of a Multi-group SEIR Model
TS. Nguyễn Ngọc Doanh (ĐHBKHN)
TS. Đoàn Thái Sơn (Viện Toán học)
5. 16/10/2015: Almost periodicity of differential equations: motivation, some new developments.
GS. Nguyễn Văn Minh (Columbus State University)
6. 23/10/2015: Tính ổn định vững của hệ động lực
TS. Đỗ Đức Thuận (ĐHBKHN)
7. 30/10/2015: Phương pháp nhiễu trong lý thuyết hệ động lực và một vài ứng dụng (I)
PGS. Đặng Đình Châu (ĐH KHTN-ĐHQGHN)
8. 6/11/2015: Phương pháp nhiễu trong lý thuyết hệ động lực và một vài ứng dụng (II)
PGS. Đặng Đình Châu (ĐH KHTN-ĐHQGHN)
9. 13/11/2015: Modified projection method for strongly pseudomonotone variational inequalities
NCS. Trần Việt Anh (HV Công nghệ Bưu chính Viễn thông)
10. 27/11/2015: Ngưỡng chính tắc của hàm chỉnh hình trong Cn
TS. Vũ Việt Hùng (ĐH Tây Bắc)
11. 4/12/2015: Về tính hội tụ yếu trong các không gian Hardy
TS. Lương Đăng Kỳ (ĐH Quy Nhơn)
12. 11/12/2015: TBA
13. 18/12/2015: Tính ổn định của hệ PTVP có trễ
TS. Nguyễn Trường Thanh (ĐH Mỏ-Địa chất)
Tích phân suy rộng trong các đề thi môn Giải tích KHTN-ĐHQGHN (từ 2000-2014)
Đề thi các năm: De thi GT KHTN 2000-2014
Tích phân suy rộng (Lý thuyết và lời giải các đề ): Tích phân suy rộng